Mastering SVG Arcs — 4nds Journal

9 min be taught
SVG,
Originate,
Coding

SVG arcs demystified! Akshay Gupta explains the technique to grasp radii, rotation, and arc path to create lovely curves. Invent arcs a formidable half of your SVG toolkit for creating extra dynamic, intricate designs with self assurance.

So, I esteem drawing birds with code. Inspired by my brother’s admire for birdwatching, I love the strong point of their feathers, colors, and sounds. But what I scrutinize most is the manner their bodies curve and a quantity of birds can bag dramatically a quantity of curves! So, I took my admire for drawing with SVG graphics and frail it to experiment with chicken shapes. Over time, I’ve drawn enough to alter into incredibly adept at working with arc shapes.

Five examples of birds drawn in SVG, including a peacock, robin, parakeet, parrot, and toucan. — (Wide preview)

Listed below are about a of my contemporary works. Inspired by designs I got here all over on Dribbble, I created my versions with code. That it is advisable to presumably browse thru the code for each on my CodePen.

But sooner than we dive into creating curves with arcs, please close here and look at out Myriam Frisano’s contemporary article, “SVG Coding Examples: Critical Recipes For Writing Vectors By Hand.” It’s an magnificent primer to the SVG syntax and this will come up with accurate context heading into the ideas we’re holding here by manner of mastering SVG arcs.

A Swiftly SVG Refresher

You in all likelihood know that SVGs are crisp, infinitely scalable illustrations without pixelated degradation — vectors for the salvage! What which that it is advisable to not know is that few builders write SVG code. Why? Effectively, the syntax appears to be like to be like advanced and routine compared to, jabber, HTML. But belief me, when you destroy it down, it’s not simplest doable to hand-code SVG however also somewhat somewhat of stress-free.

Let’s make certain that you simply’re as much as speed on the SVG viewBox since it’s a key belief by manner of the scalable half of *SVG. We’ll spend the analogy of a digicam, lens, and canvas to point to this belief. Imagine your browser window as a digicam and the SVG viewBox as the digicam lens specializing within the painting of a chicken you’ve created (the SVG). Imagine the painting on a smartly-organized canvas that will stretch some distance beyond what the digicam captures. The viewBox defines which half of this canvas is visible thru the digicam.

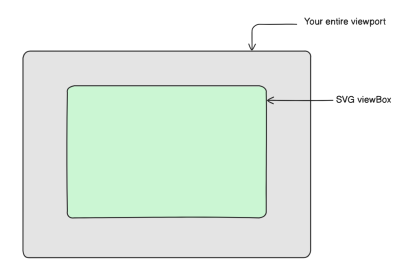
Illustrating the viewBox in inexperienced, esteem a digicam lens. — (Wide preview)

Let’s jabber we bag now an SVG component that we’re sizing at 600px sq. with width and height attributes without delay on the component.

Let’s flip our consideration to the viewBox attribute:

The viewBox attribute defines the interior coordinate plan for the SVG, with four values mapping to the SVG’s x, y, width, and height in that divulge.

Here’s how this relates to our analogy:

Camera Space and Dimension
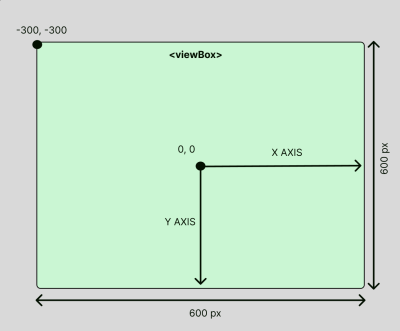
The -300, -300 represents the digicam lens’ left and top edge insist. In the intervening time, 600 x 600 is esteem the digicam’s frame dimension, exhibiting a explicit fragment of that house.
Unchanging Canvas Dimension
Changing the x and y values adjusts the build the digicam points, and width and height govern how noteworthy of the canvas it frames. It doesn’t resize the accurate canvas (the SVG component itself, which remains at 600×600 pixels). No matter the build the digicam is positioned or zoomed, the canvas itself remains mounted.

So, even as you adjust the viewBox coordinates, you’re simply deciding on a brand unique discipline of the canvas to focal point on without resizing the canvas itself. This permits you to govern the visible discipline without changing the SVG’s accurate veil dimensions.

Demonstrating coordinates for the head-left nook (-300,-300), center (0,0), and the route of x and y axis (left to fair exact and top to backside respectively) of the viewBox. — (Wide preview)

You now bag the context you’ll need to be taught to work with aspects in SVG, which is the build we launch working with arcs!

The Component

We bag an component. And we’re viewing the component’s contents thru the “lens” of a viewBox.

A enables us to diagram shapes. We produce other aspects for drawing shapes — particularly , , and — however imagine being restricted to strict geometrical shapes as an artist. That’s the build the customized component is accessible in. It’s frail to diagram advanced shapes that can not be created with the accepted ones. Imagine as a flexible container that enables you to mix’n’match a quantity of drawing instructions.

With a single , which that it is advisable to mix multiple drawing instructions into one refined, ravishing contain. Today, we’re specializing in a huge explicit route say: arcs. In other phrases, what we’re doing is drawing arc shapes with .

Here’s a transient, no-frills instance that areas a all the diagram thru the instance we regarded at earlier:


   
    fill="transparent"
    stroke="black"
    stroke-width="24"
  />



Be taught about the Pen [Arc path animation [forked]](https://codepen.io/smashingmag/pen/bNbeQQy) by akshaygpt.
Be taught about the Pen Arc route animation [forked]  by akshaygpt.
Now, I get it. Taking a behold at that string of numbers for the first time is esteem staring into the Matrix, fair exact? But when you get the hold of it, you’ll seek that arcs aren’t as frightening as they behold.
Let’s destroy down the  in that instance. We’ll destroy it down even further within the following half, however for now:

M 0 0  strikes the scamper to the center of the viewBox however doesn’t if truth be told “diagram” one thing else horny yet.
A 100 100 0 1 1 200 0  attracts an arc with a radius of 100 in both the X and Y axes, ending at (200, 0).

That it is advisable to presumably visualize the coordinate positions in red resulting from a quantity of M instructions within the following demo:

Be taught about the Pen[ArcProbabilitiesb/w2points[ArcPossibilitiesb/w2points[forked]](https://codepen.io/smashingmag/pen/EaYyOGW) by akshaygpt.
Be taught about the Pen Arc Probabilities b/w 2 points [forked]  by akshaygpt.
Be taught about that? We bag two points along the X-axis which could very smartly be relative to the viewBox’s center, and a crooked line connects them. Now, know that the numbers in an M say are setting coordinates, and the numbers in an A say diagram a line along the SVG’s axes. You horny drew a curve in SVG!
Dissecting An Arc
We can zoom into the M and A instructions even further to raised designate what’s going on.


First off, we’re working with an arc, or extra precisely, an elliptical arc, which is a crooked line. We know that a supreme circle is merely an ellipse with equal radii in both the X and Y directions. We can switch the form of the circle by giving it a quantity of, unmatching radii values.
Here's what we all know up to now:

M

0: Coordinate along the X-axis.
0: Coordinate along the Y-axis.


A

100: Radius tag within the X route.
100: Radius tag within the Y route.
200: The arc’s endpoint within the X-route.
0: The arc’s endpoint within the Y-route.



There are three values within the A say that we salvage of skipped. These are esteem “switches” within the sense that they are Boolean values that enable or disable obvious issues about the arc.

0: Rotates the arc along the X-axis.
1: Determines whether or not here's a “small” arc (0) with a span higher than 180° or a “smartly-organized” arc (1) with a span higher than 180°.
1: Gadgets whether or not the arc “sweeps” in a clockwise route or a counter-clockwise route, the build 0 equals clockwise and 1 equals counter-clockwise.

If we rob this knowledge and re-write the  with these definitions, then it begins to come together extra clearly:




Presumably we are able to simplify that somewhat the spend of abbreviations:


(Wide preview)
Let’s rob this knowledge and launch taking half in with values to behold the diagram in which it behaves.
Visualizing The Probabilities
All over again, if here's the  we’re starting up with:


Then, we are able to manipulate it in myriad techniques. Mathematically speaking, which that it is advisable to create an endless collection of arcs between any two points by adjusting the parameters. Listed below are about a diversifications of an arc that we get when all we manufacture is switch the arc’s endpoints within the X () and Y () directions.

Be taught about the Pen[ArcProbabilitiesb/w2points[ArcPossibilitiesb/w2points[forked]](https://codepen.io/smashingmag/pen/WbexYLV) by akshaygpt.
Be taught about the Pen Arc Probabilities b/w 2 points [forked]  by akshaygpt.
Or, let’s administration the arc’s width and height by updating its radius within the X route () and the Y route (). If we mess around with the  tag, we are able to manipulate the arc’s height:

Be taught about the Pen[Rx[Rx[forked]](https://codepen.io/smashingmag/pen/xbKOQMr) by akshaygpt.
Be taught about the Pen Rx [forked]  by akshaygpt.
In the same diagram, we are able to manipulate the arc’s width by updating the  tag:

Be taught about the Pen[Ry[Ry[forked]](https://codepen.io/smashingmag/pen/mybEQvG) by akshaygpt.
Be taught about the Pen Ry [forked]  by akshaygpt.
Let’s seek what occurs when we rotate the arc along its X-axis (). This parameter rotates the arc’s ellipse around its center. It gained’t have an effect on circles, however it indubitably’s a sport-changer for ellipses.

Be taught about the Pen[x-axis-rotation[x-axis-rotation[forked]](https://codepen.io/smashingmag/pen/VYZjVRx) by akshaygpt.
Be taught about the Pen x-axis-rotation [forked]  by akshaygpt.
Even with a attach build of endpoints and radii ( and ), and a given attitude of rotation, four clear arcs can connect them. That’s because we bag now the  flag tag that would be one of two values, as smartly as the  flag that is also one of two values. Two boolean values, each with two arguments, give us four clear chances.

Be taught about the Pen[4circumstances[4cases[forked]](https://codepen.io/smashingmag/pen/wBwWQOb) by akshaygpt.
Be taught about the Pen 4 circumstances [forked]  by akshaygpt.
And lastly, adjusting the arc’s endpoint along the X () and Y () directions shifts the arc’s build without changing the total form.

Be taught about the Pen[endxendy[endxendy[forked]](https://codepen.io/smashingmag/pen/xbKOQeL) by akshaygpt.
Be taught about the Pen endx, endy [forked]  by akshaygpt.
Wrapping Up
And there you bag it, SVG arcs demystified! Whether or not you’re manipulating radii, rotation, or arc route, you now bag the full tools to grasp these lovely curves. With discover, arcs will change into horny yet any other half of your SVG toolkit, person that offers you the flexibility to create extra dynamic, intricate designs with self assurance.
So bag taking half in, bag experimenting, and quickly you’ll be bending arcs esteem a pro — making your SVGs not horny functional however beautifully inventive. Must you enjoyed this dive into arcs, drop a esteem or allotment it along with your mates. Let’s bag pushing the boundaries of what SVG can manufacture!


(gg, yk)

Mastering SVG Arcs — 4nds Journal

A Swiftly SVG Refresher

The Component

Dissecting An Arc

Visualizing The Probabilities

Wrapping Up

Leave a Reply Cancel Reply

Email Newsletters!